
ようこそ!日野第六小学校Webサイトへ


学年・専科だより
カテゴリ:専科だより
音楽科のこのごろ
こんにちは。音楽科の佐々木です。
新型コロナウイルス感染症対策をどうしよう・・・といつも考えさせられる日々です。
9月より、3~5年生リコーダー学習を再開しました。

ポツリ・ポツリと席が空いています。
なぜかというと、クラス人数の半数は音楽室リコーダー集中学習(20分間)。
え!?あと半数は?
というと、教室で学習しています(20分間)。担任の先生、見守りありがとう。
私が事前に撮影した動画を見ながら、歌意を調べたり聴音クイズに挑戦したりして学習を進めています。
そして、授業の途中で児童が交代します。
【児童の反応】
少人数のリコーダー学習が集中できてよかった。
少ない人数だと音の重なりが聴き取りやすい。
マスクを外せる時間が、ちょっぴりうれしい!

3年生は、早くリコーダーの学習をしたくてたまらなかったようです。
確かに!1学期に配布しているのに、ずっとお預け状態!
自分の楽器だもの!音出したいよね。
今、シ→ラ→ソまで学習をしました。
11月からは、高いドや高いレを学習する予定です。

6年生は「沖縄メドレー」を合奏中。
リコーダー隊は、廊下の壁に向かって練習。
みんな同じ方向を向いてる!新しいスタイルです。
沖縄の軽快なメロディを合奏して、「沖縄旅行したいなぁぁぁぁぁ!」と今の状況が早く終息することを願っています。
理科「植物の実や種子のでき方」5年生
5年生になってから、初めての理科室の学習になりました。
顕微鏡を使って、花の花粉を観察しました。
おしべから花粉をつけたプレパラートを顕微鏡でのぞいてみると・・・
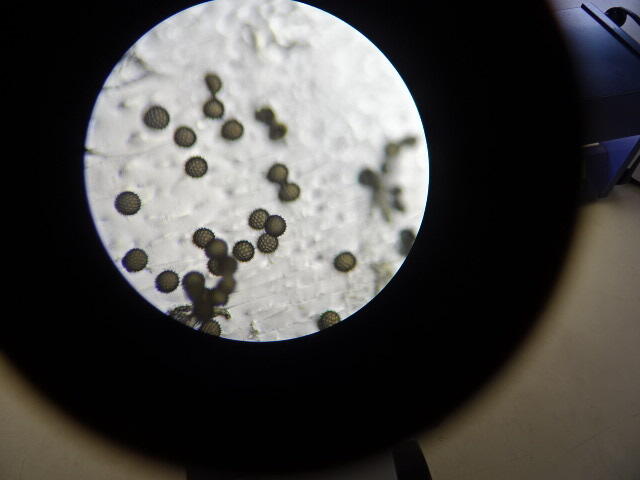
見えました!
顕微鏡をのぞいて見える世界にびっくりの子どもたちでした!
(写真は、学校に咲いているヒルガオの花粉です。)
顕微鏡を使って、花の花粉を観察しました。
おしべから花粉をつけたプレパラートを顕微鏡でのぞいてみると・・・

見えました!
顕微鏡をのぞいて見える世界にびっくりの子どもたちでした!
(写真は、学校に咲いているヒルガオの花粉です。)
Mr.Horieです
みなさんこんにちは!Mr. Horieです。
私事ですが、夏休み中、外国語指導における専門性をより深めるため、第二言語習得理論の本を読みました。そこで、少し気になる記述がありましたので、こちらで共有させていただきたいと思います。
私が読んだ書物では、バイリンガル(二言語併用者)の利点等について、以下のように記述されていました。
・「バイリンガルの子どもは、ひとつの言語しかしゃべらない子どもに比べて、認知能力が優れている」
・「この場合の認知能力というのは、創造性、類推能力、柔軟な情報処理能力などを示すが、さらに、最近の研究で、母語と外国語の距離が遠いほうが認知能力の優位性が高いというのがある」
・「バイリンガルの老人は認知症の発症が遅れ、その後の進行も特に早いということはない」
上記はあくまでも「バイリンガルに関する」記述ですが、少なくとも英語を学習することは一般的に脳にとってよいことのように感じました。2点目に関して言えば、日本語と英語の距離は、そこまで近くはないと考えますので、英語を学ぶことは認知能力を育成する上で効果があるのではないか、と個人的には興味深く思えました。
機会があれば、このような話を子どもたちにもしてあげたいと思います。
それでは、本学期もよろしくお願いいたします。
図工の授業にて
今年は展覧会の予定です。
5年生は6月から作品作りが始まりました。
ボンドを使って生き物を描き、丁寧に絵の具で塗っていきます。
迫力のある作品に仕上がりそうです。

5年生は6月から作品作りが始まりました。
ボンドを使って生き物を描き、丁寧に絵の具で塗っていきます。
迫力のある作品に仕上がりそうです。

専科算数 学びのたね「なんで??」
6年生との授業での一コマでした。
先日、分数同士のかけ算の学習をしている際に、
どうすれば計算できるかという課題を考えていました。
直前の分数×整数の学習で
「分数にかけるときにはかけられる数の分子にかける数をかける」
と学習していたので、きっと子供たちは
「同じように、分子にかけてみればいいんだ!」という発想で解いてみるかな
とほんの少し思っていました。
しかし、予想したことではありましたが
「分母同士、分子同士をかける」という、計算の方法をとっている子が
たくさんいました。
事前に教科書を読んでみていたり、塾で教わっていたりなどして
やり方を知っている子がやはりたくさんいるのですね。
でも、そんな多くの子に
「なんで分母同士、分子同士でかけるの?」と聞くと
意外と答えられない子が多かったです。
やり方や解き方は知っていても
「なぜ、その計算方法が成り立つのか」という仕組みが分かっていない
という子が一定数いるんだなということが、わかりました。
ぜひ、本当に使える力として「仕組み」をしっかり理解しておけば
もしも解き方などを忘れてしまっても、
改めて自力で導き出すことができるかなと思います。
「なんで?」という学びのたねを見つけて
仕組みを理解しておくと、本当の力になるのかなと思っています。
お読みいただいている皆さんも、
中学・高校時代に習ったはずの公式、どんな仕組みで成り立っているか覚えていますか?
自分も自信がないので、週末の息抜きに数学の教科書を
改めて開けてみようかな。
先日、分数同士のかけ算の学習をしている際に、
どうすれば計算できるかという課題を考えていました。
直前の分数×整数の学習で
「分数にかけるときにはかけられる数の分子にかける数をかける」
と学習していたので、きっと子供たちは
「同じように、分子にかけてみればいいんだ!」という発想で解いてみるかな
とほんの少し思っていました。
しかし、予想したことではありましたが
「分母同士、分子同士をかける」という、計算の方法をとっている子が
たくさんいました。
事前に教科書を読んでみていたり、塾で教わっていたりなどして
やり方を知っている子がやはりたくさんいるのですね。
でも、そんな多くの子に
「なんで分母同士、分子同士でかけるの?」と聞くと
意外と答えられない子が多かったです。
やり方や解き方は知っていても
「なぜ、その計算方法が成り立つのか」という仕組みが分かっていない
という子が一定数いるんだなということが、わかりました。
ぜひ、本当に使える力として「仕組み」をしっかり理解しておけば
もしも解き方などを忘れてしまっても、
改めて自力で導き出すことができるかなと思います。
「なんで?」という学びのたねを見つけて
仕組みを理解しておくと、本当の力になるのかなと思っています。
お読みいただいている皆さんも、
中学・高校時代に習ったはずの公式、どんな仕組みで成り立っているか覚えていますか?
自分も自信がないので、週末の息抜きに数学の教科書を
改めて開けてみようかな。
学びの礎・六小の子
教育課程
令和7年度の教育課程です。
学校経営重点計画
令和7年度のプロジェクトシートです。
令和7年度の学校経営重点計画です。
令和6年度の学校経営重点計画(評価)です。
Netモラル(保護者向け)
日野市GIGAスクール構想
検索
カウンタ
4
3
0
6
6
4
6
お知らせ
保健室からの連絡
インフルエンザや新型コロナウイルス感染症等でお休みし、主治医より登校許可が出ましたら、下のリンクページ内にあります登校許可書をご提出ください。
◆登校許可書.pdf

