2020年10月の記事一覧

先日の問題の解説です．

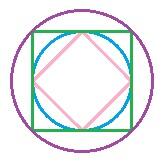
下の図を参照しながらお読みください．

ピンクの正方形は青の円の内側にぴったりで，

緑の正方形は青の円の外側にぴったりです．

このとき，２つの正方形の面積を比べると

青の円の直径×青の円の直径÷２＝ピンクの正方形

青の円の直径×青の円の直径　　＝緑の正方形

となります．

つまり，緑の正方形はピンクの正方形の２倍の面積になるということがわかります．

そんな緑の正方形の外側にぴったりの円（紫）をかくと，

面積の比を考えれば，ピンクの正方形：青の円＝緑の正方形：紫の円なので

青の円のちょうど２倍の面積になることがわかります．

大人の考えを使うと「半径をルート２倍にしないといけないから…」

と考えてしまいがちですが，

実は小学校でこれまで積み重ねてきた考え方を駆使すると，

出来てしまうのです．