
ようこそ!日野第六小学校Webサイトへ


学年・専科だより
カテゴリ:専科だより
音楽科のこの頃
こんにちは。音楽の佐々木です。今年度もよろしくお願いします。
学校再開後、本校では体育館を音楽室として使用してきました。
鑑賞やリズム打ちによる参加型で進めています。
が・・・しかし。「暑い!」です。
熱中症が心配!
となりまして、7月6日より音楽室でできる限りのソーシャルディスタンスを確保して進めていくこととなりました。
さて、音楽科のこの頃です。
【3~6年共通】


イェッセル作曲の「おもちゃの兵隊の行進」にリズム打ちを付けて、楽しみながら音楽のよさを感じています。
【3年生】
①弦楽器の楽器を学習し、ベートーヴェン作曲の「メヌエット」を鑑賞しました(踊りながら)。
②金管楽器の楽器を学習し、ルロイ=アンダーソン作曲の「トランペット吹きの休日」を鑑賞しました(変化する旋律の部分を立ち座りしながら)。
周りの教室への迷惑を考えることなく、動きまくり、盛り上がりまくりながらの授業です。
【4年生】
①3年生で学び残したビゼー作曲の「ファランドール」を鑑賞しました。
異なるせんりつが重なる部分では、「3人の王の行進」がよく聞こえる人と「馬のおどり(ファランドール舞曲)」がよく聞こえる人がいて、個々に聴き方が違うことを感じました。
②金管楽器を学習し、ルロイ=アンダーソン作曲の「トランペット吹きの休日」を鑑賞し、変化する旋律クイズに全問正解する人がたくさんでました。
【5年生】
①ショスタコーヴィチ作曲の「祝典序曲」をオーケストラと吹奏楽で聞き比べました。弦楽器の華やかさが好きな人、吹奏楽の温かみのある音が好きな人で好みが分かれました。
②現在、モーツァルト作曲の「アイネクライネナハトムジーク第1楽章」を鑑賞中です。弦楽合奏なので、演奏形態の違いを絶賛味わい中。
【6年生】
①ホルスト作曲の「木星」を鑑賞しました。深いところから込み上げてくるような旋律と楽器の音色に魅了されました。
②現在、「ラバースコンチェルト」にボイスパーカッション伴奏を作成中です。お互いに交流できる日がくることを願っています。
音楽科の最近
【3年生】「えんそうのくふう」
いろいろな楽器を学習、始めました。
リコーダー「山のポルカ」に他の楽器の音色を重ねようということで、3年生のために合奏譜を用意しました。

木琴、鉄琴をグループに分かれて体験中の3年生。一人が打鍵し、まわりの児童が旋律を歌います。鍵盤の位置やマレットの持ち方など、互いにアドバイスしながら進めることができています。木琴好きと鉄琴好きに好みが分かれはじめました。今後に期待です。
【4年生】「日本の伝統的な楽器に親しもう」
箏で「さくら さくら」を演奏しています。

①爪合わせ
②グループでの学習の進め方(役割分担等)
③正しい姿勢で、筝の音色を味わいながら学習進行中
「意外と弾けるかも!」「前より音が響くようになった!」
色々な弾き方のコツを覚えてます。
早く桜の時期になって欲しいですね。
【5年生】「豊かな表現をもとめて」
威風堂々のリコーダー奏をとても頑張った5年生に、やりたがっていた「ルパン三世のテーマ」合奏をご褒美学習。

39人でリコーダー、鍵盤ハーモニカ、低音、ピアノ、シンセサイザー、グロッケン、鉄琴、木琴、シェーカー、カウベル、トライアングル、タンブリン、ボンゴ、サスペンテッド・シンバル(ビブラスラップも)を分担し、自分のパートを絶賛譜読み中です。
これまでの学習を生かし、同じパートで学び合ったり、少しできるようになると、近くにいるパートと声を掛け合って合わせるようになりました。
全体の合奏では、全体の音のバランスや曲想の変化や強弱の変化が演奏に表れるといいなと思います。
いろいろな楽器を学習、始めました。
リコーダー「山のポルカ」に他の楽器の音色を重ねようということで、3年生のために合奏譜を用意しました。

木琴、鉄琴をグループに分かれて体験中の3年生。一人が打鍵し、まわりの児童が旋律を歌います。鍵盤の位置やマレットの持ち方など、互いにアドバイスしながら進めることができています。木琴好きと鉄琴好きに好みが分かれはじめました。今後に期待です。
【4年生】「日本の伝統的な楽器に親しもう」
箏で「さくら さくら」を演奏しています。

①爪合わせ
②グループでの学習の進め方(役割分担等)
③正しい姿勢で、筝の音色を味わいながら学習進行中
「意外と弾けるかも!」「前より音が響くようになった!」
色々な弾き方のコツを覚えてます。
早く桜の時期になって欲しいですね。
【5年生】「豊かな表現をもとめて」
威風堂々のリコーダー奏をとても頑張った5年生に、やりたがっていた「ルパン三世のテーマ」合奏をご褒美学習。

39人でリコーダー、鍵盤ハーモニカ、低音、ピアノ、シンセサイザー、グロッケン、鉄琴、木琴、シェーカー、カウベル、トライアングル、タンブリン、ボンゴ、サスペンテッド・シンバル(ビブラスラップも)を分担し、自分のパートを絶賛譜読み中です。
これまでの学習を生かし、同じパートで学び合ったり、少しできるようになると、近くにいるパートと声を掛け合って合わせるようになりました。
全体の合奏では、全体の音のバランスや曲想の変化や強弱の変化が演奏に表れるといいなと思います。
外国語通信3
こんにちは。Mr.Horieです。
今回は写真がありませんが、英語を勉強する上で少し役立つお話をしたいと思います。
みなさん、アルファベットの各文字(A,B,CからZまで)には「名前」と「音」があることをご存知でしょうか。
私は学生時代、「名前」と「音」を真剣に意識せず、英語を学んでいました。しかし、約2年半前の海外派遣研修で外国語の教授法を学んだことが、「名前」と「音」を真剣に意識しながら英語と向き合うようになった大きなきっかけとなりました。
「名前」と「音」について、文字のAを題材にざっと説明すると
Aの名前…「エイ」
Aの音 …「ア」
となります。
※英語の発音を片仮名表記するのは不可能ですが、便宜上、使用しています。
各文字の中には「音」を複数もっているものもありますが、児童に指導する場合は、「最もよく用いられる音」を教えるようにしていますし、外国語の教授法においてそれが定石と言われています。
「音」への理解が深まると、初めて読む単語に出会った際に、その言葉の発音を類推しやすくなるとともに、綴り、発音、口形とをリンクさせながら学習ができるので、語彙を増やすことに役立ちます。
ですので、英語を学習する際には、まず「音」への理解を深めることをおすすめいたします。実際に私も、「音」を学習してから、語彙をより広げることができています。
4年生 まぼろしの花
「こんな花があったらいいな・・・」と
イメージを広げて、大きな紙にのびのびと描いています。
まぼろしの花の種も紙粘土で作りました。

専科算数 学んだことを使って…
少し前まで6年生は「比例」についての学習をしていました。
学習したことを活用する活動を先日行いました。
「教室の前に置かれた大量の紙束の枚数を求める」という活動です。
闇雲に数えてみるのではなく、
「10枚の重さは何グラムだろう」「10枚の厚みは何センチだろう」
また「1センチで何枚だろう」などという発想から全体をはかればよい
というように色々な考え方が出てきました。
「1グラムで何枚だろう」という意見には
「それって量れるの?」という的確なツッコミも出て
活発に議論も行われました。
実際に自分たちなりのやり方で数えたりはかったりして
枚数を考えました。
でも、考えるだけに終わらず最後にはやっぱり「数えてみたい」
という意見も多く出たので、みんなで手分けして数えることに。
コンピュータの表計算ソフトに一人一人が数えた枚数を打ち込み
合計を出す命令を入れるとあっという間に合計が出てきました。
2クラスやったうち、誤差が少なかったクラスでは
合計が出た瞬間「おー!!」と歓声が上がっていました。
算数で学んだことが日常のどんな場面で生きているのか
そんな視点が少しでももてるとよいなと考えています。


学習したことを活用する活動を先日行いました。
「教室の前に置かれた大量の紙束の枚数を求める」という活動です。
闇雲に数えてみるのではなく、
「10枚の重さは何グラムだろう」「10枚の厚みは何センチだろう」
また「1センチで何枚だろう」などという発想から全体をはかればよい
というように色々な考え方が出てきました。
「1グラムで何枚だろう」という意見には
「それって量れるの?」という的確なツッコミも出て
活発に議論も行われました。
実際に自分たちなりのやり方で数えたりはかったりして
枚数を考えました。
でも、考えるだけに終わらず最後にはやっぱり「数えてみたい」
という意見も多く出たので、みんなで手分けして数えることに。
コンピュータの表計算ソフトに一人一人が数えた枚数を打ち込み
合計を出す命令を入れるとあっという間に合計が出てきました。
2クラスやったうち、誤差が少なかったクラスでは
合計が出た瞬間「おー!!」と歓声が上がっていました。
算数で学んだことが日常のどんな場面で生きているのか
そんな視点が少しでももてるとよいなと考えています。


アンサンブル演奏のために
【4年生】
リコーダーの高いミの指づかいを習いました。
「もののけ姫」の曲でリコーダー二重奏の演奏に取り組んでいます。

自分たちでパートを決めたり、個人練習・パート練習・グループ練習をしたりするのは初めてですが、時間を見ながら活動を進めています。
演奏の完成が楽しみですね。
【6年生】
運動会の練習や準備に追われる中、休み時間を活用してアルトリコーダー・テナーリコーダー・バスリコーダーの担当者が、自主練習に現れました。

連合音楽会ではリコーダー四重奏に挑戦します。早く全員で音を重ねたいらしく、「2段目まで合わせてみよう」「3段目からやってみよう」と声をかけ合いながら進めています。
アンサンブルの楽しさを味わいながら、自主練習をしている姿が、とても立派な6年生です。
図工の授業にて
アート・カードを活用した鑑賞の授業を行いました。
マッチングゲームという、2枚の作品の共通する項目を探すゲームをしているところです。

マッチングゲームという、2枚の作品の共通する項目を探すゲームをしているところです。

きまぐれ演奏会(放課後)
こんにちは。音楽専科の佐々木です。
6月28日(金)の放課後に、5・6年生対象で「きまぐれ演奏会 vol.2」を催しました。今回は、ミュージカル界に進路希望している若い歌手2人をお呼びし、独唱・重唱をしました。
会に興味をもってくれている約40名の児童に囲まれて、演奏会が成功しました。
今年は、学芸会の年ですね。
どんな表情で、どんな歌い方で表現したらよいのか、参考になっているといいです。

「きまぐれ演奏会」なので、次回の日程は未定ですが、弦楽器でゲストを呼べたらと考えています。
6月28日(金)の放課後に、5・6年生対象で「きまぐれ演奏会 vol.2」を催しました。今回は、ミュージカル界に進路希望している若い歌手2人をお呼びし、独唱・重唱をしました。
会に興味をもってくれている約40名の児童に囲まれて、演奏会が成功しました。
今年は、学芸会の年ですね。
どんな表情で、どんな歌い方で表現したらよいのか、参考になっているといいです。

「きまぐれ演奏会」なので、次回の日程は未定ですが、弦楽器でゲストを呼べたらと考えています。
外国語通信1
みなさん、こんにちは。
Mr.Horieです。
本年度初めての外国語通信ということで、児童が使用している教材について紹介したいと思います。
児童が使用している教材は、デジタル教材とリンクしています。デジタル教材は、リスニングなどの課題はもちろん、アルファベットの書き方や、文字の音や名前を学ぶ歌など、様々な領域をカバーしています。それらに加え、世界の国々の人々の暮らしの様子や風土など、異文化に触れることのできる映像も盛り込まれています。
外国語の学習は、英語そのものに加えて、異文化理解も大切なテーマの一つです。学習を通して、異文化及び人権への理解がさらに深まるよう、指導していきます。

Mr.Horieです。
本年度初めての外国語通信ということで、児童が使用している教材について紹介したいと思います。
児童が使用している教材は、デジタル教材とリンクしています。デジタル教材は、リスニングなどの課題はもちろん、アルファベットの書き方や、文字の音や名前を学ぶ歌など、様々な領域をカバーしています。それらに加え、世界の国々の人々の暮らしの様子や風土など、異文化に触れることのできる映像も盛り込まれています。
外国語の学習は、英語そのものに加えて、異文化理解も大切なテーマの一つです。学習を通して、異文化及び人権への理解がさらに深まるよう、指導していきます。

41×41 解説編
先日ご紹介しました
「41×41の簡単な計算の仕方」について
先日お会いした保護者の方に
「気になります、早く知りたいです。」と
嬉しいお声を頂きました。
というわけで甚だ簡単ではありますが解説です。
下の図をご覧下さい。
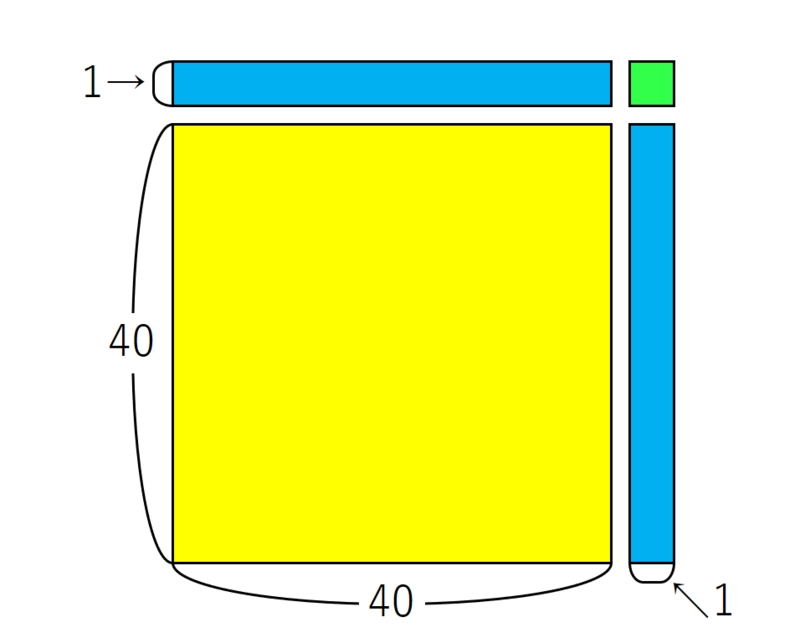
41×41をこの様に捉えます。
そこから
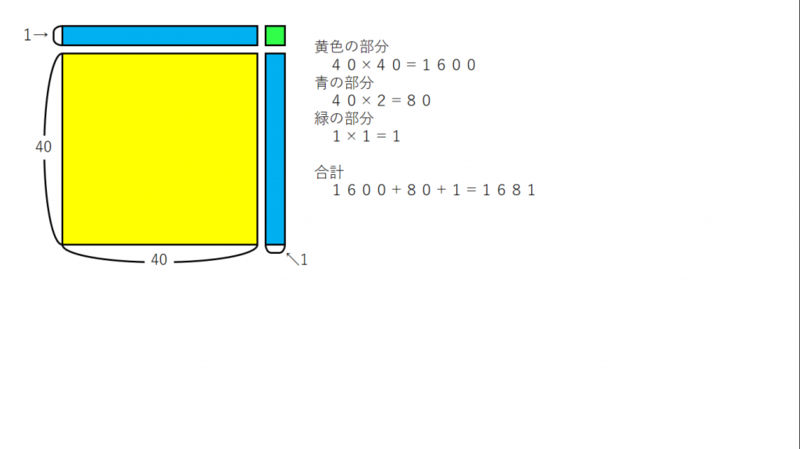
と考えると、あら不思議。
前回の記事で紹介した「展開」の構図が出来上がるという仕組みです。
小学生の理屈を使っても
「40×40+40×2+1×1」へ変形することが可能なのです。
子ども達の中からも
「これなら簡単に暗算ができそう。」という声が聞こえました。
時々、授業に来る子ども達には話をすることですが、
算数を上手に使える場面は生活の中で様々な場面にあります。
そこに気付けるか気付けないは、意外と大きな差になるかも知れません。
小学校の算数は、そこに気付くための鍵をたくさん手に入れる勉強です。
と考えてみると、捨てたもんじゃないなと思えませんか。
「41×41の簡単な計算の仕方」について
先日お会いした保護者の方に
「気になります、早く知りたいです。」と
嬉しいお声を頂きました。
というわけで甚だ簡単ではありますが解説です。
下の図をご覧下さい。

41×41をこの様に捉えます。
そこから

と考えると、あら不思議。
前回の記事で紹介した「展開」の構図が出来上がるという仕組みです。
小学生の理屈を使っても
「40×40+40×2+1×1」へ変形することが可能なのです。
子ども達の中からも
「これなら簡単に暗算ができそう。」という声が聞こえました。
時々、授業に来る子ども達には話をすることですが、
算数を上手に使える場面は生活の中で様々な場面にあります。
そこに気付けるか気付けないは、意外と大きな差になるかも知れません。
小学校の算数は、そこに気付くための鍵をたくさん手に入れる勉強です。
と考えてみると、捨てたもんじゃないなと思えませんか。
学びの礎・六小の子
教育課程
令和7年度の教育課程です。
学校経営重点計画
令和7年度のプロジェクトシートです。
令和7年度の学校経営重点計画です。
令和6年度の学校経営重点計画(評価)です。
Netモラル(保護者向け)
日野市GIGAスクール構想
検索
カウンタ
4
3
0
4
1
6
9
お知らせ
保健室からの連絡
インフルエンザや新型コロナウイルス感染症等でお休みし、主治医より登校許可が出ましたら、下のリンクページ内にあります登校許可書をご提出ください。
◆登校許可書.pdf

